Kubikkmeterhuset 5.-10. Trinn Oppgave 4: Areal og Problemløsing
Trinn: 5.-10.
Mål: Problemløsing ved bruk av forskjellige matematiske innfallsvinkler
Begreper:
Utstyr: Papir og blyant
Fra Fagfornyelsen 6. trinn: Bruke ulike strategiar for å rekne ut areal og omkrins og utforske samanhengar mellom desse.
9. trinn: Utforske eigenskapane ved ulike polygonar og forklare omgrepa formlikskap og kongruens utforske, beskrive og argumentere
Oppgave
1. Samle elevene ved stråleflateveggen og be dem om å finne noen trekanter.
2. Spør om de kan bestemme arealet til noen av disse trekantene uten å måle.
3. La dem diskuterer i små grupper. Hver gruppe presenterer en løsning. Her er noen trekanter som det er lett å finne arealene av ved å bruke enkelte geometriske begreper:
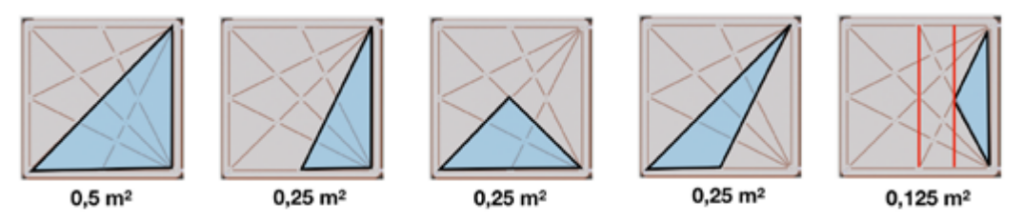
Det er mange måter å finne disse arealene på. Den enkleste er kanskje å tenke på arealene som en brøk av det hele. Trekantformelen kan også brukes: A = 1/2 * b * h.
4. Finn arealene til noen trekanter som ikke er så lett å finne arealet av. Dette er et eksempel på en trekant dere kan begynne med:
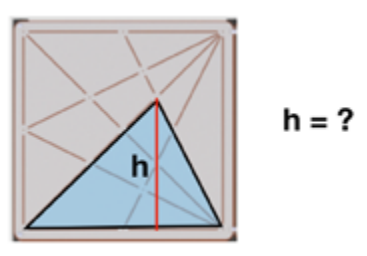
Løsning
Elevene presenterer sine løsninger til klassen. Forhåpentligvis har klassen funnet flere forskjellige måter å løse oppgaven på.
Denne trekanten har arealet 1/3 m2. Her er noen forslag til en måte å løse oppgaven på:
Med geometri: Sammenlign disse to trekantene. Vinklene blir de samme fordi topp- og bunnlinjer er parallelle. Trekantene er formlike. Siden lengdene i basene er i forholdet 2:1, vil alle andre lineære målinger blir i forholdet 2:1.
Den store trekanten har da en høyde som er 2 ganger så høy som den lille trekanten. Til sammen er de en meter. h + 2h = 1, da blir høyden til den store trekanten 2/3.
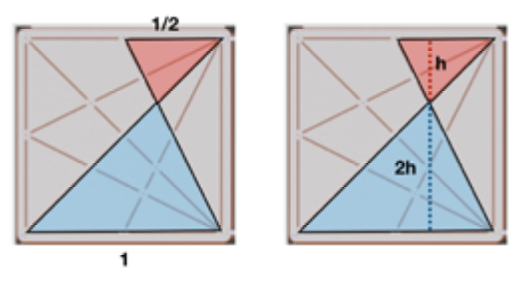
Med koordinater: Tegn akser med origo i nederst venstre hjørnet av designet. Topp-punktet til trekanten ligger i skjæringspunktet av to linjer med likninger nedenfor.
y = x og y = -2x + 2
Løs systemet for å finne {x, y} = {2/3, 2/3}. Da har trekanten høyden 2/3 meter og areal 1/3 m2