Kubikkmeterhuset 5.-10.. Trinn Oppgave 1: Sirkelens Omkrets

Introduksjon

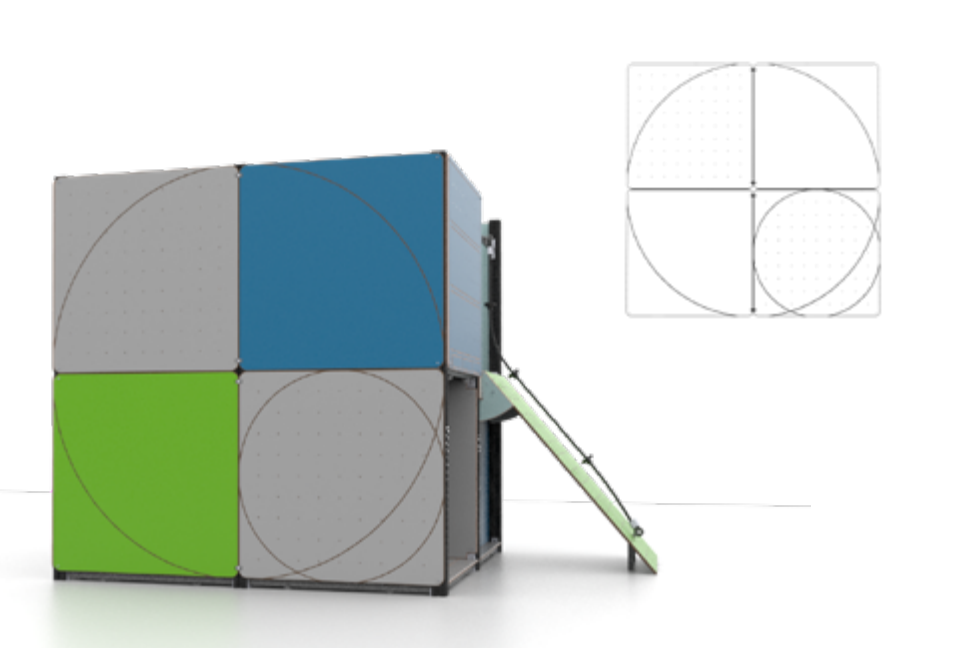
Kubikkmeterhus – Sirkelvegg

De to sirklene på denne sideflaten kan brukes til måling av sirkelens omkrets og areal. Oppgave 1 og 2 kan gjøres sammen eller separat. Dersom dere gjør begge oppgavene, kan dere sammenligne de ulike måtene π (ca. 3,14) forekommer i både lengde- og arealmålinger. π er lett å misforstå, spesielt om elevene pugger formler som bruker π utenat, det er lettere å forstå sammenhenger med fysiske modeller og målingsbegreper.

Oppgave

1. Samle elevene ved sirkelveggen. Sikre at elevene er kjent med begrepet “omkrets” ved å spørre dem hva omkretsen til en av kvadratmeter-platene på veggen er.

2. Diskuter omkretsen i forhold til meter, dm og cm. Ved bruk av meterstokken kan du vise at omkretsen til en av platene er 4 meter.

3. Likedan kan du bruke en desimeter-stav for å vise at omkretsen er 40 dm. Hvor mange centimeter er det rundt omkretsen til platen? (400)

4. Be elevene om å gjøre et overslag over omkretsen til sirklene.

5. Del elevene inn i grupper.

6. Gruppene skal finne omkretsen til begge sirklene, både den store og den lille. De skal også finne ut hvor mange ganger større omkretsen til den store er ift. til den lille. Elevene kan bruke desimeterstaver for å måle rundt sirklene.

Tips: Gå på jakt etter sirkler i ulike størrelser og bruk målebåndet til å måle omkretsen og diameteren av sirklene. Dette er en aktivitet du kan gjøre både ute og inne. Finn sykkelhjul, kumlokk, trillebårhjul, bunnen av ei bøtte eller en tallerken som har form som en sirkel osv… mål sirklenes omkrets og diameter og noter resultatene. Elevene kan komme til å bli veldig overrasket når de ser at uansett størrelse på sirkelen og sammenligner med diameteren, finner forholdet mellom dem, så vil svaret alltid ligge rundt 3+litt til!

Løsning

Gjenta for elevene at den lille sirkelen har omkrets cirka 314 cm, 31,4 dm eller 3,14 meter. Bruk en meterstokk og vis at diameteren er nøyaktig 1 meter. Be 2 elever om å bøye meterstokken langs kanten av sirkelen og bruk den for å telle hvor mange ganger meteren går rundt sirkelen. Fremhev at omkretsen er 3,14 diameter. Dette er et nøkkelbegrep i sammenheng med sirkelmåling. Omkretsen til en sirkel er π ganger diameteren. Den store sirkelen har omkrets 628 cm = 62,8 dm = 6,28 m. Sjekk at omkretsen til den store sirkelen også er 3,14 ganger så lang som diameteren. Omkretsen til den store sirkelen er 2 ganger så lang som omkretsen til den lille sirkelen. Når en form er skalert n ganger, er alle lineære målinger også skalert n ganger. (Alle todimensjonale målinger, som areal, er skalert n² ganger og alle volum-målinger er skalert n³ ganger.)